Basics

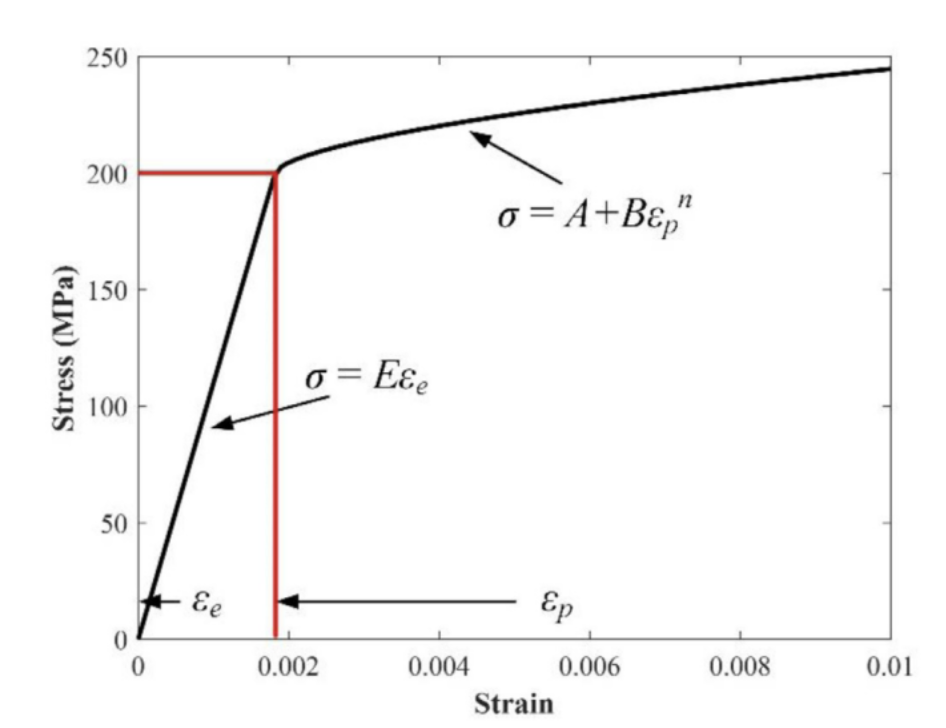
Strain is defined as the amount of relative deformation caused by a force acting on an object, whereas stress is defined as the force acting per unit area of an object. A stress-strain curve for a material provides the relationship between stress and strain in engineering. It is obtained by gradually applying load to a test coupon and measuring the deformation to determine the stress and strain.

Stress v/s Strain

Almost all metals behave like elastic objects over a specific range. This range varies for different metals and is affected by factors such as mechanical properties, atmospheric exposure (corrosion), grain size, heat treatment, and working temperature.

Initially, the material follows Hooke's law. The strain will be proportional to stress. It means that the ratio of stress to strain will be a constant (Young's Modulus of Elasticity).

As the material moves towards plastic region of deformation, the relationship of stress-strain would follow the equation : σ = a+bε^(n), where σ is the stress, ε is the plastic strain. a, b, n are the constants of the expression of plastic behavior.

Now We have created a model which analyses and predicts this graph using various ML techniques. Wanna Try it?

Let's Try it! Github Documentation

Shear Stress v/s Shear Strain

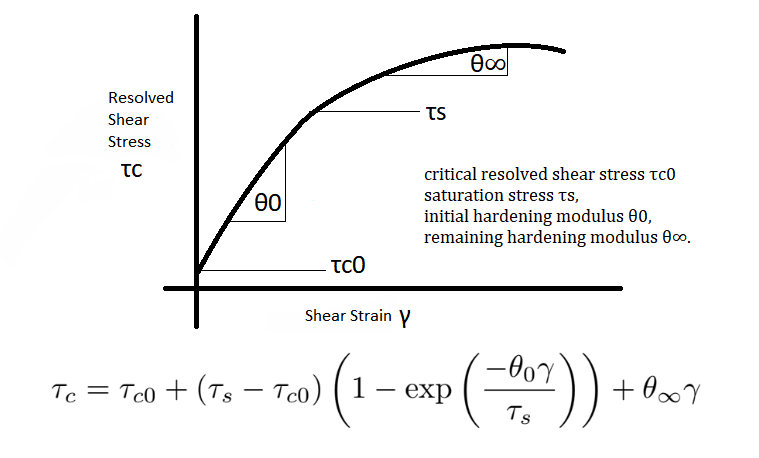
The material behaviour is modeled by a single-crystal elastic-viscoplastic model based on isomorphic elastic ranges. The plastic transformation P describes the change of lattice vectors in the elastic law due to slip. At room temperature, the sample material shows a bcc crystal structure. Slip occurs if the resolved shear stress, τ^α=ĈT^~2PK. Shear-rates are calculated by the viscous ansatz of Hutchinson (1976) and two additional material parameters are needed.

The strain-rate sensitivity m is derived from strain-rate experiments for a polycrystalline mild steel ES. The critical resolved shear stress is described by τ_c = τ_c0 + (τ_s - τ_c0)( 1 - exp(-θ₀γ/τ_s) + θ_∞γ, where τ_c0 is critical resolved shear stress, τ_s is saturation stress, θ₀ is initial hardening modulus, θ_∞ is a remaining hardening modulus and γ is shear strain. This model has been implemented in a user subroutine (UMAT) of the finite element code ABAQUS.

Enough explanation, time to visualize

Let's Try it! Github Documentation

Practical Analysis of Stress-Strain

Materials science:

Stress-strain analysis is commonly used in materials science to study the properties of different materials, such as metals, polymers, and ceramics. This information can be used to design new materials with improved properties, or to optimize the performance of existing materials.

Engineering:

It is widely used in engineering to design and test structures and mechanical components. Engineers can use stress-strain analysis to determine the maximum load that a structure or component can withstand, and to predict its behavior under different types of loads.

Biomechanics:

Stress-strain analysis is used in biomechanics to study the behavior of biological tissues and structures, such as bones and joints. This information can be used to design medical implants, such as hip replacements, that are durable and safe for use in the human body.

Aerospace:

It is used extensively in aerospace engineering to design and test aircraft and spacecraft components. This includes everything from the materials used to construct the vehicles, to the shape and design of the components themselves.

Automotive:

Stress-strain analysis is used in the automotive industry to design and test components such as engines, transmissions, and suspension systems. Engineers can use stress-strain analysis to optimize the performance of these components, as well as to ensure their safety and durability.